針對現有的S型齒廓修形方法存在的問題,設計了一種新的齒廓曲線設計方法。該方法通過使用嚙合矩陣實現共軛點的快速求解,并基于共軛點對齒廓曲線進行修形。計算結果表明,改進法設計下的齒廓相比于傳統S型齒廓具有更小、更均勻的側隙,嚙合區間得到增大,傳動誤差有所降低,提高了齒廓的嚙合性能,能夠滿足高精度場合下的使用要求。
諧波減速器具有減速比大、結構簡單、精度高等優點,因此被廣泛應用于機器人、航空航天和軍事等對于精度要求較高的領域。目前在嚙合理論方面,主流的方法有基于Willis定理的包絡法、改進運動學法和瞬心線法。在諧波傳動齒廓方面主要出現過直線齒廓、漸開線齒廓、圓弧齒廓及S型齒廓。直線齒廓是諧波傳動的發明者Musser提出的,但該齒形沒有考慮柔輪的變形所引起的位移與轉角誤差。漸開線齒廓的研究已趨于成熟,但在諧波運動的嚙合過程中由于共軛嚙合區域較小,且會產生尖點嚙合情況,這些會造成接觸點應力的急劇增大,大幅縮短齒廓壽命。圓弧齒廓是目前國內研究最多的齒廓齒形,與漸開線齒廓相比,其具有嚙合齒數多的優點, 改善了應力狀況與嚙合質量,但雙圓弧齒廓的側隙不均勻,部分區域存在側隙較大的情況。S型齒廓由日本學者Ishikawa等在1989年基于齒條近似法提出,根據映射關系可以實現與同類齒廓的連續接觸。但這類齒廓大多都是在無窮齒數下的近似設計,并未考慮實際運動過程中的轉角影響。基于此,本文綜合考慮了諧波傳動的彈性變形、齒輪偏轉角、波發生器類型等因素,根據運動件的幾何關系和嚙合矩陣,通過曲線映射的方式得到原始凸齒廓,根據改進法對原始齒廓進行修形,接著根據修形完成的凸齒廓求解兩段凹齒廓,并最終與傳統S型齒廓進行對比。
柔輪與剛輪間轉角關系:固定波發生器坐標系,并以波發生器的回轉中心o為原點,長軸為y軸,建立坐標系,則波發生器、柔輪、剛輪之間的運動關系如圖1所示。
 為了方便計算,本文的波發生器將采用余弦曲線,根據柔輪中性層的不變形理論,可以將其看作波發生器的等距曲線,則柔輪中性層曲線在極坐標下可以表示為
為了方便計算,本文的波發生器將采用余弦曲線,根據柔輪中性層的不變形理論,可以將其看作波發生器的等距曲線,則柔輪中性層曲線在極坐標下可以表示為

式中:k為徑向變形系數,m為模數,rm為柔輪的中性層半徑。
rm大小可以通過柔輪分度圓半徑求解:

波發生器裝配后迫使柔輪發生變形,其中柔輪輪齒的法向轉角可以表示為

根據中性層不伸長理論,其柔輪變形后轉過的弧長應與未變形前掃過的弧長保持一致,因此有
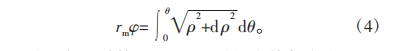
為了便于計算,因此整理時忽略其高階項,通過計算其一階近似積分可以得到

根據理論傳動比可以得到

其余的轉角關系可以通過圖1中的幾何關系可得:

傳動齒廓設計:根據齒條近似法原理,當剛輪的齒數無窮大時,此時柔輪將相對于剛輪沿著運動軌跡平移。圖2為齒條近似原理圖,其中AB曲線為柔輪相對于剛輪的運動軌跡,將A點作為映射的起始點,將B點作為映射的結束點,按照0.5倍的比例進行曲線映射,得到了剛輪凸齒廓BC與柔輪凸齒廓AC,由于曲線映射的關系,柔輪與剛輪齒廓均保留了運動軌跡的特征,即柔輪凸齒廓與剛輪凸齒廓間將實現連續嚙合。其中柔輪中性層在剛輪坐標下的運動軌跡AB 的軌跡方程表示為:


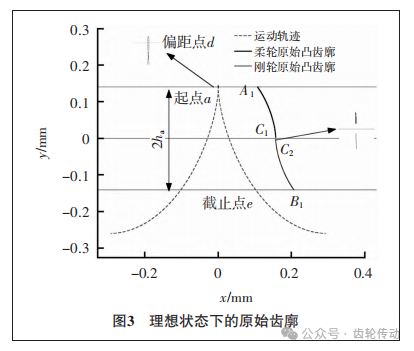
由于原始曲線在(-π/2,π/2)內的運動軌跡存在偏距點,考慮到齒廓間連接的順滑性,因此設計段內不能包含凹凸性突變的情況,因此映射的起始角度ηd應取運動軌跡二階導數為0時對應的點,假設偏距點為d,則e為曲線映射的截止點,其角度可以表達為ηe=arccos(1-2h*a /k),其中h*a為齒頂高系數。因此原始剛輪凸齒廓表達式為:
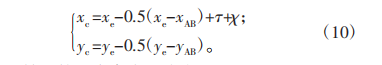
原始柔輪凸齒廓表達式為:

傳統齒廓修形:在求解原始齒廓時,做了柔輪與剛輪的齒數均是無限的假設,然而在實際運動過程中,柔輪齒廓除了沿著運動軌跡平移外還存在齒廓本身的旋轉角度,因此需要對原始齒廓進行修形。根據坐標系之間的轉化原則,一開始的原始曲線M是建立在中性層上面的,而柔輪的齒頂相對于剛輪的運動軌跡則需要建立在柔輪的分度圓上,因此運動軌跡M0需要在原始曲線M的基礎上向上平移一段h。h可以表示為

傳統的修形方法是假設理想嚙合條件下柔輪齒廓與剛輪齒廓的嚙合點為P,但由于轉角影響的存在,柔輪在嚙合點P處沿著N旋轉了ζ,從而柔輪與剛輪齒廓將產生干涉,干涉量可以通過嚙合點P的位移PB來表示。如圖4所示,F點為柔輪原始齒廓法線與中心線的交點,由于旋轉角度ξ較小,因此點P在轉角ξ的影響下產生的位移PB可以用弧長FA代替,其表達式為

式中,lNF為線段NF的長度。
lNF的表達式為

式中:(xP,yp )為P點坐標,(xN,yN )為N點坐標,α為接觸點壓力角。
α的計算公式為


因為ξ較小,于是將上述弧長FA近似看作齒廓x方向上的修型量,將其定義為Δx,將變形量平均分配給剛輪與柔輪,原始曲線的映射初始角為ηd,映射結束角度為ηe,因此柔輪齒頂輪廓的表達式為:

剛輪的齒頂輪廓表達為:

根據齒條近似法,柔輪與剛輪的凹齒廓同樣可以通過凸齒廓的映射所得到,但為了保證柔輪與剛輪齒廓嚙合的過程中不產生干涉,要在映射的齒廓上加入間隙調整量,于是柔輪的凸齒廓表達式為:
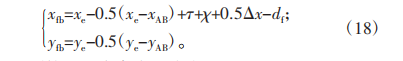
剛輪的凸齒廓表達式為:

由于映射起始點并不為0,因此凹齒廓與凸齒廓間存在空白區域,需要通過過渡直線連接,通過剛輪與柔輪兩端齒廓的端點,可以得到過渡直線段表達式:

式中,(xd1,yd1)和(xd2,yd2)為凸齒廓與凹齒廓表達式的端點。
傳統的S型齒廓修形方法嚙合區域較小,且側隙在嚙和區間內變化較大,難以滿足對精度要高的場合,因此本文提供了一種新的修形方式來解決這些問題。
改進法齒廓修形:根據齒輪嚙合原理中的坐標系變換原理,柔輪固定坐標系可通過坐標系變化矩陣Mcf和底矢變化矩陣Wcf變化到剛輪坐標系,其中矩陣Mcf和矩陣Wcf表示為:

而剛輪坐標系轉換到柔輪坐標系的坐標變換矩陣Mfc和底矢變換矩陣Wfc分別表示為:

根據上述表達的矩陣,我們可以得到柔輪齒廓坐標在剛輪固定坐標系下的坐標表達式為

同樣的剛輪齒廓坐標點在柔輪坐標系中的坐標表達式為

為了分析原始柔輪凸齒廓相對于剛輪的運動狀態,直觀地反映裝配后諧波傳動齒廓的嚙合情況,在將柔輪凸齒廓與剛輪凸齒廓分別轉換到各自坐標系后使用嚙合矩陣Mcf,得到了圖5所示的(0,π)區間內柔輪的運動軌跡圖。
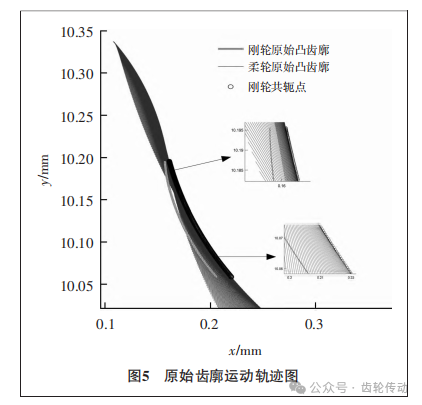
通過boundary函數查找柔輪運動軌跡的邊緣輪廓,通過處理可以得到剛輪的共軛點。將剛輪的共軛齒廓與剛輪的原始齒廓間的差值作為修形量進行第一次修形。假設剛輪的共軛曲線的橫坐標為xca1,則修形量可以表示為

那么第一次修形后柔輪齒頂輪廓的表達式為:

剛輪的齒頂輪廓表達式為:

將第一次修形后的柔輪齒廓與剛輪齒廓再次代入嚙合矩陣Mcf中,并再次查看嚙合情況。

我們發現經過第一次修形后剛輪凸齒廓末端嚙合情況較好,而初始端的側隙較大。這是因為修形時齒廓末端所采用的共軛點是由柔輪凸齒廓末端所構成的,因此將此處的修形量均分給2段原始齒廓是合理的。然而初始端的共軛點并非由柔輪原始凸齒廓的初始端所構成,因此在此處將其作為修形量不合理。針對這種情況,采取對齒廓進行二次修形的方式來降低初始段的側隙。同樣使用boundary函數提取出剛輪的共軛點,假設此時剛輪的共軛曲線的橫坐標為xca2 ,則修形量表示為

那么經過二次修形后柔輪的齒頂輪廓表達式為:
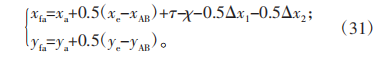
剛輪的齒頂輪廓表達為:
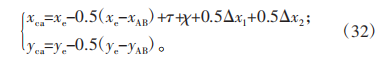
將二次修形后的柔輪齒廓代入嚙合矩陣Mcf,查看剛輪初始段的側隙情況。

通過圖7可以看到剛輪初始端依然存在過度修形的情況,但此時上端的側隙分布已經處于0.5μm以下,屬于合理范圍之內,故不再對凸齒廓進行第三次修形。至此,柔輪與剛輪的凸齒廓修形完畢。根據修形后的剛輪凸齒廓,通過使用嚙合矩陣 Mfc,采用剛輪包絡柔輪的方法,計算出剛輪的運動軌跡。同樣采用boundary函數提取柔輪的共軛點,通過這種方式,可以得到與剛輪凸齒廓共軛的柔輪凹齒廓。

用上述的方法同樣可以求解剛輪凹齒廓,基于柔輪的運動軌跡,通過柔輪凸齒廓求解剛輪的共軛凹齒廓。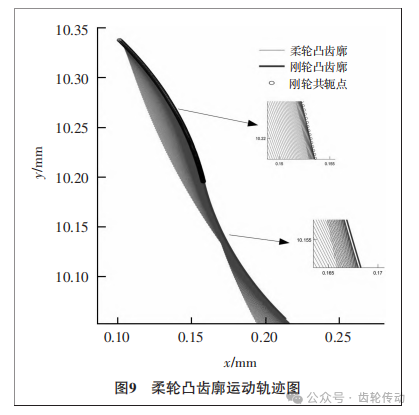
表2為本文齒廓設計的參數,下面將對本文提到的兩種平面設計的齒廓進行嚙合性能分析,主要從傳動側隙、共軛區域及瞬時傳動比展開分析。
側隙分析:柔輪的嚙合狀態的好壞可以大致通過齒廓側隙這個指標來判斷。從側隙的大小與分布可以初步判斷傳動過程中穩定性,齒間載荷分布于是否產生干涉。首先建立側隙計算模型。通過將齒廓曲線離散成點,求解當波發生器旋轉過一定角度下時,每個柔輪齒廓與剛輪齒廓間的最小距離即為側隙lfc。
 通過圖11的左側可以看到凸齒廓與凹齒廓間存在空白區域,這是由于初始映射角非零導致的,因此在最終的齒廓中使用直線過渡段將兩段齒廓連接。因為剛輪與柔輪的凹齒廓是在凸齒廓的基礎上施加間隙調整量后得到的,因此剛輪與柔輪齒廓在完全嚙合狀態下間隙均勻穩定。
通過圖11的左側可以看到凸齒廓與凹齒廓間存在空白區域,這是由于初始映射角非零導致的,因此在最終的齒廓中使用直線過渡段將兩段齒廓連接。因為剛輪與柔輪的凹齒廓是在凸齒廓的基礎上施加間隙調整量后得到的,因此剛輪與柔輪齒廓在完全嚙合狀態下間隙均勻穩定。

由于通過改進法修形后得到的齒廓曲線在凸齒廓頂端存在一定的過度修形,因此在完全嚙合狀態下兩齒廓的間隙呈現出中間大、兩邊小的趨勢。由于改進法的凹齒廓是根據共軛點求得的,因此沒有明顯的連接空白區域。
從圖13可以看出,與傳統法相比,改進法設計下的齒廓側隙整體更小,且更加平穩。傳統S型齒廓設計方法由于凹齒廓是直接由凸齒廓映射所得,因此在嚙合區整體側隙偏大,而在嚙入區的側隙則有所下降。由于改進法設計下的S型齒廓在凸齒廓初始端存在一定的過度修形,因此在嚙合區的側隙相對于嚙入區有所上升,但上升的幅度較小,整體側隙分布情況趨于穩定,在一定程度上提高了回轉精度。

嚙合區域分析:柔輪齒廓與剛輪齒廓的嚙合大致可以分為2個區域:1)嚙合區。此時柔輪凸齒廓與剛輪凹齒廓間會產生嚙合,與此同時柔輪凹齒廓與剛輪凸齒廓同樣將發生接觸。2)嚙入區。柔輪凸齒廓與剛輪凸齒廓間在這個區間內將產生嚙合,此區域也是諧波傳動的主要嚙合區。因此計算嚙合區間時需要進行分段求解。 兩種修形方法計算出的嚙合區間如圖14所示。 由于傳統修形法的凹齒廓采用直接映射的方式,因此凸齒廓與凹齒廓在嚙合的過程中不發生接觸,因此在整個運動過程中只有兩段凸齒廓發生共軛,因此該設計方法下只有一段嚙合區間。而改進法下的凹齒廓是根據運動軌跡包絡求得的,因此即使是在嚙合區內也有較好的接觸情況。兩種修形方法均在[9.334°,55.645°]的區間內發生共軛,而通過改進法設計的柔輪齒廓,在[2.154°,7.18°]區間實現了兩點共軛,與此同時柔輪的凸齒廓在[2.154°,8.975°]和 [9.334°,55.645°]區間上分別實現了與剛輪凹齒廓與凸齒廓間的嚙合,實現了二次共軛,證明了改進法設計的齒廓增大了共軛區域,降低了柔輪嚙合過程中的軸向應力,提高了傳動效率,使得傳動更加可靠,在一定程度上延長了減速器的使用壽命。

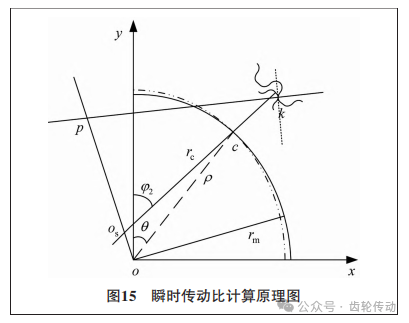
瞬時傳動比:通過平均積分角速度求得的傳動比只能從宏觀角度上描述諧波減速器的運動狀況,但實際上諧波減速器的瞬時傳動比是變化的。瞬時傳動比的波動會直接影響減速器運行的穩定性,而傳動比誤差既來源于中性層曲線的形狀也取決于齒廓曲線。如圖15所示,當波發生器固定時,若柔輪非變形端以恒定角速度ω1回轉,則在變形端上的點c將以瞬時角速度ω1c圍繞中性層曲線在c點處的曲率中心os 回轉,由于線速度相等,故有
 若剛輪的角速度設為ω2,此時的瞬時傳動比將表示為
若剛輪的角速度設為ω2,此時的瞬時傳動比將表示為

其中,i為理論傳動比,其大小為

根據Willis定理,若兩齒廓的接觸點為k,則經過k點的公法線與瞬時回轉中心連接線oos的交點p就是瞬時嚙合節點。故嚙合節點的瞬時傳動比可以表示為

因為兩種修形方法均采用相同的中性層曲線,故原始曲線誤差相同。通過式(34)和式(36)可以發現瞬時傳動比的波動幅度在一定程度上與瞬時曲率中心直接關聯,通過計算發現中性層半徑越大,徑向變形量越小,瞬時傳動比就越趨于穩定。
由于諧波減速器多齒嚙合的特性,其傳動誤差將會被均化,因此對求解得到的瞬時傳動比曲線積分后進行疊加。計算后發現改進法設計下的齒廓傳動誤差為3.96%,而傳統修S型齒廓誤差為3.962%。相對于傳統S型齒廓,改進法設計下的齒廓傳動誤差略有降低,性能提升了約0.05%,這也意味著齒廓曲線對于瞬時傳動比的影響較小。同時在誤差曲線積分時發現,嚙合齒數也是影響傳動誤差的關鍵因素。隨著嚙合齒數的增加,原始曲線的誤差將逐漸趨向于0,此時傳動誤差將主要體現為齒廓曲線誤差,整體的傳動誤差將得到明顯的降低。
本文提出了一種區別于傳統S型齒廓設計的方法。與傳統S型齒廓相比,改進法設計的S型齒廓具有側隙更小、共軛區間更大、傳動誤差更小的特點,可以滿足高精度場合下的使用要求。由于柔輪的軌跡曲線存在偏距,為了保證齒廓曲線連接的順滑性,齒廓的映射設區域應不包含曲線上凹凸性突變的點,即映射起點應為運動軌跡二階導數為0的點,且為了保證原始齒廓有足夠的映射區域與齒廓間的平滑連接,變形系數k的取值范圍應在[0.9,1.1]內。齒廓的類型對瞬時傳動比的影響較小,而中性層曲線的類型,中性層半徑與徑向變形量對瞬時傳動比的影響較大,在設計時應優先考慮大半徑、小變形量的設計方案。

作業來說,精度較高,所以該控制器可實現良好的軌跡跟蹤控制。
本文針對飛機牽引系統的自動控制問題進行研究,設計了基于Fareh控制策略的非線性控制器,通過控制牽引點的速度大小與方向來實現飛機的軌跡跟蹤與姿態調節。通過MATLAB/Simscape對系統進行仿真模擬,驗證了所設計控制器的可行性。
參考文獻:略。
0 引言
諧波減速器具有減速比大、結構簡單、精度高等優點,因此被廣泛應用于機器人、航空航天和軍事等對于精度要求較高的領域。目前在嚙合理論方面,主流的方法有基于Willis定理的包絡法、改進運動學法和瞬心線法。在諧波傳動齒廓方面主要出現過直線齒廓、漸開線齒廓、圓弧齒廓及S型齒廓。直線齒廓是諧波傳動的發明者Musser提出的,但該齒形沒有考慮柔輪的變形所引起的位移與轉角誤差。漸開線齒廓的研究已趨于成熟,但在諧波運動的嚙合過程中由于共軛嚙合區域較小,且會產生尖點嚙合情況,這些會造成接觸點應力的急劇增大,大幅縮短齒廓壽命。圓弧齒廓是目前國內研究最多的齒廓齒形,與漸開線齒廓相比,其具有嚙合齒數多的優點, 改善了應力狀況與嚙合質量,但雙圓弧齒廓的側隙不均勻,部分區域存在側隙較大的情況。S型齒廓由日本學者Ishikawa等在1989年基于齒條近似法提出,根據映射關系可以實現與同類齒廓的連續接觸。但這類齒廓大多都是在無窮齒數下的近似設計,并未考慮實際運動過程中的轉角影響。基于此,本文綜合考慮了諧波傳動的彈性變形、齒輪偏轉角、波發生器類型等因素,根據運動件的幾何關系和嚙合矩陣,通過曲線映射的方式得到原始凸齒廓,根據改進法對原始齒廓進行修形,接著根據修形完成的凸齒廓求解兩段凹齒廓,并最終與傳統S型齒廓進行對比。
1 S型齒的齒廓設計
柔輪與剛輪間轉角關系:固定波發生器坐標系,并以波發生器的回轉中心o為原點,長軸為y軸,建立坐標系,則波發生器、柔輪、剛輪之間的運動關系如圖1所示。

式中:k為徑向變形系數,m為模數,rm為柔輪的中性層半徑。
rm大小可以通過柔輪分度圓半徑求解:
波發生器裝配后迫使柔輪發生變形,其中柔輪輪齒的法向轉角可以表示為
根據中性層不伸長理論,其柔輪變形后轉過的弧長應與未變形前掃過的弧長保持一致,因此有
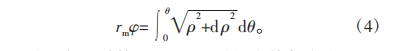
為了便于計算,因此整理時忽略其高階項,通過計算其一階近似積分可以得到
根據理論傳動比可以得到

其余的轉角關系可以通過圖1中的幾何關系可得:

表1 諧波傳動各角度參數含義


傳動齒廓設計:根據齒條近似法原理,當剛輪的齒數無窮大時,此時柔輪將相對于剛輪沿著運動軌跡平移。圖2為齒條近似原理圖,其中AB曲線為柔輪相對于剛輪的運動軌跡,將A點作為映射的起始點,將B點作為映射的結束點,按照0.5倍的比例進行曲線映射,得到了剛輪凸齒廓BC與柔輪凸齒廓AC,由于曲線映射的關系,柔輪與剛輪齒廓均保留了運動軌跡的特征,即柔輪凸齒廓與剛輪凸齒廓間將實現連續嚙合。其中柔輪中性層在剛輪坐標下的運動軌跡AB 的軌跡方程表示為:

由于原始曲線在(-π/2,π/2)內的運動軌跡存在偏距點,考慮到齒廓間連接的順滑性,因此設計段內不能包含凹凸性突變的情況,因此映射的起始角度ηd應取運動軌跡二階導數為0時對應的點,假設偏距點為d,則e為曲線映射的截止點,其角度可以表達為ηe=arccos(1-2h*a /k),其中h*a為齒頂高系數。因此原始剛輪凸齒廓表達式為:
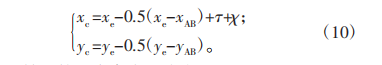
原始柔輪凸齒廓表達式為:


2 齒廓修形
傳統齒廓修形:在求解原始齒廓時,做了柔輪與剛輪的齒數均是無限的假設,然而在實際運動過程中,柔輪齒廓除了沿著運動軌跡平移外還存在齒廓本身的旋轉角度,因此需要對原始齒廓進行修形。根據坐標系之間的轉化原則,一開始的原始曲線M是建立在中性層上面的,而柔輪的齒頂相對于剛輪的運動軌跡則需要建立在柔輪的分度圓上,因此運動軌跡M0需要在原始曲線M的基礎上向上平移一段h。h可以表示為
傳統的修形方法是假設理想嚙合條件下柔輪齒廓與剛輪齒廓的嚙合點為P,但由于轉角影響的存在,柔輪在嚙合點P處沿著N旋轉了ζ,從而柔輪與剛輪齒廓將產生干涉,干涉量可以通過嚙合點P的位移PB來表示。如圖4所示,F點為柔輪原始齒廓法線與中心線的交點,由于旋轉角度ξ較小,因此點P在轉角ξ的影響下產生的位移PB可以用弧長FA代替,其表達式為
式中,lNF為線段NF的長度。
lNF的表達式為
式中:(xP,yp )為P點坐標,(xN,yN )為N點坐標,α為接觸點壓力角。
α的計算公式為

因為ξ較小,于是將上述弧長FA近似看作齒廓x方向上的修型量,將其定義為Δx,將變形量平均分配給剛輪與柔輪,原始曲線的映射初始角為ηd,映射結束角度為ηe,因此柔輪齒頂輪廓的表達式為:

剛輪的齒頂輪廓表達為:

根據齒條近似法,柔輪與剛輪的凹齒廓同樣可以通過凸齒廓的映射所得到,但為了保證柔輪與剛輪齒廓嚙合的過程中不產生干涉,要在映射的齒廓上加入間隙調整量,于是柔輪的凸齒廓表達式為:
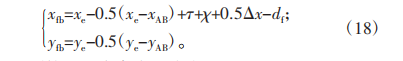
剛輪的凸齒廓表達式為:

由于映射起始點并不為0,因此凹齒廓與凸齒廓間存在空白區域,需要通過過渡直線連接,通過剛輪與柔輪兩端齒廓的端點,可以得到過渡直線段表達式:

式中,(xd1,yd1)和(xd2,yd2)為凸齒廓與凹齒廓表達式的端點。
傳統的S型齒廓修形方法嚙合區域較小,且側隙在嚙和區間內變化較大,難以滿足對精度要高的場合,因此本文提供了一種新的修形方式來解決這些問題。
改進法齒廓修形:根據齒輪嚙合原理中的坐標系變換原理,柔輪固定坐標系可通過坐標系變化矩陣Mcf和底矢變化矩陣Wcf變化到剛輪坐標系,其中矩陣Mcf和矩陣Wcf表示為:

而剛輪坐標系轉換到柔輪坐標系的坐標變換矩陣Mfc和底矢變換矩陣Wfc分別表示為:

根據上述表達的矩陣,我們可以得到柔輪齒廓坐標在剛輪固定坐標系下的坐標表達式為

同樣的剛輪齒廓坐標點在柔輪坐標系中的坐標表達式為

為了分析原始柔輪凸齒廓相對于剛輪的運動狀態,直觀地反映裝配后諧波傳動齒廓的嚙合情況,在將柔輪凸齒廓與剛輪凸齒廓分別轉換到各自坐標系后使用嚙合矩陣Mcf,得到了圖5所示的(0,π)區間內柔輪的運動軌跡圖。

通過boundary函數查找柔輪運動軌跡的邊緣輪廓,通過處理可以得到剛輪的共軛點。將剛輪的共軛齒廓與剛輪的原始齒廓間的差值作為修形量進行第一次修形。假設剛輪的共軛曲線的橫坐標為xca1,則修形量可以表示為
那么第一次修形后柔輪齒頂輪廓的表達式為:
剛輪的齒頂輪廓表達式為:

將第一次修形后的柔輪齒廓與剛輪齒廓再次代入嚙合矩陣Mcf中,并再次查看嚙合情況。

我們發現經過第一次修形后剛輪凸齒廓末端嚙合情況較好,而初始端的側隙較大。這是因為修形時齒廓末端所采用的共軛點是由柔輪凸齒廓末端所構成的,因此將此處的修形量均分給2段原始齒廓是合理的。然而初始端的共軛點并非由柔輪原始凸齒廓的初始端所構成,因此在此處將其作為修形量不合理。針對這種情況,采取對齒廓進行二次修形的方式來降低初始段的側隙。同樣使用boundary函數提取出剛輪的共軛點,假設此時剛輪的共軛曲線的橫坐標為xca2 ,則修形量表示為
那么經過二次修形后柔輪的齒頂輪廓表達式為:
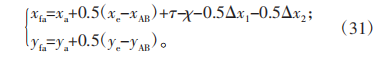
剛輪的齒頂輪廓表達為:
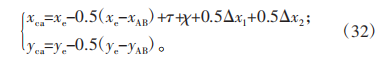
將二次修形后的柔輪齒廓代入嚙合矩陣Mcf,查看剛輪初始段的側隙情況。

通過圖7可以看到剛輪初始端依然存在過度修形的情況,但此時上端的側隙分布已經處于0.5μm以下,屬于合理范圍之內,故不再對凸齒廓進行第三次修形。至此,柔輪與剛輪的凸齒廓修形完畢。根據修形后的剛輪凸齒廓,通過使用嚙合矩陣 Mfc,采用剛輪包絡柔輪的方法,計算出剛輪的運動軌跡。同樣采用boundary函數提取柔輪的共軛點,通過這種方式,可以得到與剛輪凸齒廓共軛的柔輪凹齒廓。

用上述的方法同樣可以求解剛輪凹齒廓,基于柔輪的運動軌跡,通過柔輪凸齒廓求解剛輪的共軛凹齒廓。

表2 齒形設計與修形相關參數
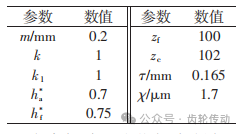

表2為本文齒廓設計的參數,下面將對本文提到的兩種平面設計的齒廓進行嚙合性能分析,主要從傳動側隙、共軛區域及瞬時傳動比展開分析。
3 齒廓分析
側隙分析:柔輪的嚙合狀態的好壞可以大致通過齒廓側隙這個指標來判斷。從側隙的大小與分布可以初步判斷傳動過程中穩定性,齒間載荷分布于是否產生干涉。首先建立側隙計算模型。通過將齒廓曲線離散成點,求解當波發生器旋轉過一定角度下時,每個柔輪齒廓與剛輪齒廓間的最小距離即為側隙lfc。


由于通過改進法修形后得到的齒廓曲線在凸齒廓頂端存在一定的過度修形,因此在完全嚙合狀態下兩齒廓的間隙呈現出中間大、兩邊小的趨勢。由于改進法的凹齒廓是根據共軛點求得的,因此沒有明顯的連接空白區域。

從圖13可以看出,與傳統法相比,改進法設計下的齒廓側隙整體更小,且更加平穩。傳統S型齒廓設計方法由于凹齒廓是直接由凸齒廓映射所得,因此在嚙合區整體側隙偏大,而在嚙入區的側隙則有所下降。由于改進法設計下的S型齒廓在凸齒廓初始端存在一定的過度修形,因此在嚙合區的側隙相對于嚙入區有所上升,但上升的幅度較小,整體側隙分布情況趨于穩定,在一定程度上提高了回轉精度。

嚙合區域分析:柔輪齒廓與剛輪齒廓的嚙合大致可以分為2個區域:1)嚙合區。此時柔輪凸齒廓與剛輪凹齒廓間會產生嚙合,與此同時柔輪凹齒廓與剛輪凸齒廓同樣將發生接觸。2)嚙入區。柔輪凸齒廓與剛輪凸齒廓間在這個區間內將產生嚙合,此區域也是諧波傳動的主要嚙合區。因此計算嚙合區間時需要進行分段求解。 兩種修形方法計算出的嚙合區間如圖14所示。 由于傳統修形法的凹齒廓采用直接映射的方式,因此凸齒廓與凹齒廓在嚙合的過程中不發生接觸,因此在整個運動過程中只有兩段凸齒廓發生共軛,因此該設計方法下只有一段嚙合區間。而改進法下的凹齒廓是根據運動軌跡包絡求得的,因此即使是在嚙合區內也有較好的接觸情況。兩種修形方法均在[9.334°,55.645°]的區間內發生共軛,而通過改進法設計的柔輪齒廓,在[2.154°,7.18°]區間實現了兩點共軛,與此同時柔輪的凸齒廓在[2.154°,8.975°]和 [9.334°,55.645°]區間上分別實現了與剛輪凹齒廓與凸齒廓間的嚙合,實現了二次共軛,證明了改進法設計的齒廓增大了共軛區域,降低了柔輪嚙合過程中的軸向應力,提高了傳動效率,使得傳動更加可靠,在一定程度上延長了減速器的使用壽命。

瞬時傳動比:通過平均積分角速度求得的傳動比只能從宏觀角度上描述諧波減速器的運動狀況,但實際上諧波減速器的瞬時傳動比是變化的。瞬時傳動比的波動會直接影響減速器運行的穩定性,而傳動比誤差既來源于中性層曲線的形狀也取決于齒廓曲線。如圖15所示,當波發生器固定時,若柔輪非變形端以恒定角速度ω1回轉,則在變形端上的點c將以瞬時角速度ω1c圍繞中性層曲線在c點處的曲率中心os 回轉,由于線速度相等,故有

其中,i為理論傳動比,其大小為
根據Willis定理,若兩齒廓的接觸點為k,則經過k點的公法線與瞬時回轉中心連接線oos的交點p就是瞬時嚙合節點。故嚙合節點的瞬時傳動比可以表示為
因為兩種修形方法均采用相同的中性層曲線,故原始曲線誤差相同。通過式(34)和式(36)可以發現瞬時傳動比的波動幅度在一定程度上與瞬時曲率中心直接關聯,通過計算發現中性層半徑越大,徑向變形量越小,瞬時傳動比就越趨于穩定。
由于諧波減速器多齒嚙合的特性,其傳動誤差將會被均化,因此對求解得到的瞬時傳動比曲線積分后進行疊加。計算后發現改進法設計下的齒廓傳動誤差為3.96%,而傳統修S型齒廓誤差為3.962%。相對于傳統S型齒廓,改進法設計下的齒廓傳動誤差略有降低,性能提升了約0.05%,這也意味著齒廓曲線對于瞬時傳動比的影響較小。同時在誤差曲線積分時發現,嚙合齒數也是影響傳動誤差的關鍵因素。隨著嚙合齒數的增加,原始曲線的誤差將逐漸趨向于0,此時傳動誤差將主要體現為齒廓曲線誤差,整體的傳動誤差將得到明顯的降低。

4 結論
本文提出了一種區別于傳統S型齒廓設計的方法。與傳統S型齒廓相比,改進法設計的S型齒廓具有側隙更小、共軛區間更大、傳動誤差更小的特點,可以滿足高精度場合下的使用要求。由于柔輪的軌跡曲線存在偏距,為了保證齒廓曲線連接的順滑性,齒廓的映射設區域應不包含曲線上凹凸性突變的點,即映射起點應為運動軌跡二階導數為0的點,且為了保證原始齒廓有足夠的映射區域與齒廓間的平滑連接,變形系數k的取值范圍應在[0.9,1.1]內。齒廓的類型對瞬時傳動比的影響較小,而中性層曲線的類型,中性層半徑與徑向變形量對瞬時傳動比的影響較大,在設計時應優先考慮大半徑、小變形量的設計方案。


作業來說,精度較高,所以該控制器可實現良好的軌跡跟蹤控制。
4 結語
本文針對飛機牽引系統的自動控制問題進行研究,設計了基于Fareh控制策略的非線性控制器,通過控制牽引點的速度大小與方向來實現飛機的軌跡跟蹤與姿態調節。通過MATLAB/Simscape對系統進行仿真模擬,驗證了所設計控制器的可行性。
參考文獻:略。
